Basic SVG animation
This topic covers basic SVG animation and is a prerequisite for Intermediate SVG Animation. Basic knowledge of HTML and JavaScript is assumed. To fully understand the material presented in this topic, plan to spend about one hour of study.
Note In order to view the examples contained within the topic, you must use a browser, such as Windows Internet Explorer 9 or later, that supports the SVG element.
- Example 1 – Basic Declarative (SMIL) Animation
- Example 2 – Basic JavaScript Animation
- Example 3 – SVG DOM Scripting
- Example 4 – No-op Transform Object
- Example 5 – Two Gears
- Example 6 – Seventeen Gears
- Example 7 – Seventeen Gears with Extended UI
- Example 8 – Seventeen Gears with Audio
- Related topics
Although not supported in Windows Internet Explorer (as described below), basic animation is straightforward when you use SVG’s declarative animation constructs ( SMIL). For example, the following code rotates a square 90 degrees over a five second interval:
Example 1 – Basic Declarative (SMIL) Animation
Live link:Example 1 (This SMIL example will not function in Internet Explorer)
<?xml version="1.0" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="800px" height="800px" viewBox="0 0 800 800"
version="1.1" xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink"> <!-- Note that this is required in order to use xlink in the <use> element. -->
<!-- THIS EXAMPLE NOT SUPPORTED IN INTERNET EXPLORER -->
<title>Simplest SVG Animation</title>
<desc>SVG declarative animation is used to rotate a square.</desc>
<!-- Create a Cartesian coordinate system (with the y-axis flipped) for the animated square.
That is, place the origin at the center of the 800 x 800 SVG viewport. -->
<g transform="translate(400, 400)">
<!-- A 200 x 200 square with the upper left-hand corner at (-100, -100). This places the center
of the square at the origin (0, 0): -->
<rect x="-100" y="-100" width="200" height="200" rx="5" ry="5"
style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;">
<animateTransform
attributeType="xml"
attributeName="transform" type="rotate"
from="0" to="90"
begin="0" dur="5s"
fill="freeze"
/>
</rect>
<line x1="-400" y1="0" x2="400" y2="0" style="stroke: black;" /> <!-- Represents the x-axis. -->
<line x1="0" y1="-400" x2="0" y2="400" style="stroke: black;" /> <!-- Represents the y-axis (although up is negative and down is positive). -->
</g>
</svg>
The previous example (as well as all the following examples) are well commented. However, a few helpful things to point out include:
- The
animateTransformelement, child of the object we want to animate (that is,rect), does all the heavy lifting and is relatively self-explanatory. - Because the square is positioned such that its center coincides with the origin of the viewport, at (400, 400), the square is rotated 90 degrees about its center. If, for example, the square were defined with x=”0” and y=”0”, as in:
<rect x="0" y="0" width="200" height="200" rx="5" ry="5" style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;">
Then the square’s upper left-hand corner (as opposed to its center) would rotate 90 degrees about the origin. Give it a try.
Although declarative animation is straightforward, it can also be limiting. In the words of David Eisenberg, author of SVG Essentials: “If you choose to use scripting to do animation, you will then have available all the interactivity features of scripting; you can make animation dependent on mouse position or complex conditions involving multiple variables.”
That is, script-based animation opens the door to simple as well as complex animation possibilities. Because of this, and for other reasons (such as CSS animations), Internet Explorer does not support declarative animation. Undeniably, there can be more work associated with script-based animation, but once these scripting techniques have been mastered, you can implement animations impossible using purely declarative animation techniques. The following example, which is the JavaScript version (in HTML5) of Example 1, shows some of these techniques:
Example 2 – Basic JavaScript Animation
Live link:Example 2
<!DOCTYPE html>
<html>
<head>
<title>JavaScript SVG Animation</title>
<meta http-equiv="X-UA-Compatible" content="IE=Edge"/> <!-- Remove this line in production. -->
</head>
<body>
<svg width="800px" height="800px" viewBox="0 0 800 800">
<g transform="translate(400, 400)"> <!-- Create a Cartesian coordinate system (with the y-axis flipped) for the animated square. That is, place the origin at the center of the 800 x 800 SVG viewport: -->
<!-- A 200 x 200 square with the upper left-hand corner at (-100, -100). This places the center of the square
at the origin (0, 0): -->
<rect id="mySquare" x="-100" y="-100" width="200" height="200" rx="5" ry="5"
style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;" />
<!-- Represents the x-axis: -->
<line x1="-400" y1="0" x2="400" y2="0" style="stroke: black;" />
<!-- Represents the y-axis (although up is negative and down is positive): -->
<line x1="0" y1="-400" x2="0" y2="400" style="stroke: black;" />
</g>
</svg>
<script>
"use strict";
/* CONSTANTS */
var initialTheta = 0; // The initial rotation angle, in degrees.
var thetaDelta = 0.3; // The amount to rotate the square about every 16.7 milliseconds, in degrees.
var angularLimit = 90; // The maximum number of degrees to rotate the square.
var theSquare = document.getElementById("mySquare");
theSquare.currentTheta = initialTheta; // The initial rotation angle to use when the animation starts, stored in a custom property.
var requestAnimationFrameID = requestAnimationFrame(doAnim); // Start the loop.
function doAnim() {
if (theSquare.currentTheta > angularLimit) {
cancelAnimationFrame(requestAnimationFrameID); // The square has rotated enough, instruct the browser to stop calling the doAnim() function.
return; // No point in continuing, bail now.
}
theSquare.setAttribute("transform", "rotate(" + theSquare.currentTheta + ")"); // Rotate the square by a small amount.
theSquare.currentTheta += thetaDelta; // Increase the angle that the square will be rotated to, by a small amount.
requestAnimationFrameID = requestAnimationFrame(doAnim); // Call the doAnim() function about 60 times per second (60 FPS), or about once every 16.7 milliseconds until cancelAnimationFrame() is called.
}
</script>
</body>
</html>
Important As opposed to including or within the block, you can configure your web development server to send the X-UA-Compatible HTTP header with IE=Edge to ensure that you are running in the latest standards mode, if you are developing on an intranet.
Script-based animation is actually relatively straightforward if you understand the basics of traditional “cartoon” animation. Animation, as you probably know, is simply a series of still images, each of which is changed incrementally, shown one right after another in quick succession:

If these six images are successively shown quickly enough, the eye will see a bouncing ball:

In this case, the bouncing ball animation is produced by repeatedly showing the six images such that each image is displayed for 100 milliseconds before moving on to the next image. The same concept is used in script-based animation. In the code for Example 2, we simply call a function that incrementally changes an image every few milliseconds. In particular, we use requestAnimationFrame to tell the browser to invoke a function, doAnim about every 16.7 milliseconds (that is, about 60 frames per second or FPS). The doAnim function rotates the square by a small amount each time it is called. Because doAnim is called every few milliseconds, the square appears to rotate smoothly. After the square has rotated angularLimit number of degrees (90° in the example), we instruct the browser to stop calling doAnim by calling cancelAnimationFrame, and the animation stops (see the code comments for more information).
Before moving on to more complex examples, it’s important to point out two styles of JavaScript coding:
- DOM L2 Scripting, and
- SVG DOM Scripting
DOM L2 Scripting is “traditional” scripting and is exemplified by building “value strings” to set various items, as in:
theSquare.setAttribute("transform", "rotate(" + theSquare.currentTheta + ")");
SVG DOM scripting is exemplified by the lack of such “value strings,” and typically sets element values numerically, as in:
mySquare.transform.baseVal.getItem(0).setRotate(mySquare.currentTheta, 0, 0);
Both lines do exactly the same thing. The only minor difference is that the setRotate method requires two values indicating a center point in which to rotate the object about (center point (0, 0) in this case). The advantage of the SVG DOM scripting style is that you do not have to build “value strings” and it can be more performant than DOM L2 scripting.
The following example is the SVG DOM scripting version of Example 2:
Example 3 – SVG DOM Scripting
Live link:Example 3
<!DOCTYPE html>
<html>
<head>
<title>JavaScript SVG Animation</title>
<meta http-equiv="X-UA-Compatible" content="IE=Edge" /> <!-- Remove this line in production. -->
</head>
<body>
<svg id="svgElement" width="800px" height="800px" viewBox="0 0 800 800"> <!-- Give the svg element a name so that we can easily access it via JavaScript. -->
<g transform="translate(400, 400)"> <!-- Create a Cartesian coordinate system (with the y-axis flipped) for the animated square. That is, place the origin at the center of the 800 x 800 SVG viewport: -->
<!-- A 200 x 200 square with the upper left-hand corner at (-100, -100). This places the center of the square
at the origin (0, 0). Give the square a name so we can easily access it via JavaScript: -->
<rect id="mySquare" x="-100" y="-100" width="200" height="200" rx="5" ry="5"
style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;" />
<!-- Represents the x-axis: -->
<line x1="-400" y1="0" x2="400" y2="0" style="stroke: black;" />
<!-- Represents the y-axis (although up is negative and down is positive): -->
<line x1="0" y1="-400" x2="0" y2="400" style="stroke: black;" />
</g>
</svg>
<script>
"use strict";
/* CONSTANTS */
var initialTheta = 0; // The initial rotation angle, in degrees.
var thetaDelta = 0.3; // The amount to rotate the square about every 16.7 milliseconds, in degrees.
var angularLimit = 90; // The maximum number of degrees to rotate the square.
/* GLOBALS */
var requestAnimationFrameID;
var mySquare = document.getElementById("mySquare");
var transformObject;
mySquare.currentTheta = initialTheta; // The initial rotation angle to use when the animation starts, stored in a custom property.
transformObject = svgElement.createSVGTransform(); // Create a generic SVG transform object so as to gain access to its methods and properties, such as setRotate().
mySquare.transform.baseVal.appendItem(transformObject); // Append the transform object to the square object, now the square object has inherited all the transform object's goodness.
requestAnimationFrameID = requestAnimationFrame(doAnim); // Start the animation loop.
function doAnim() {
var transformObject;
if (mySquare.currentTheta > angularLimit) {
cancelAnimationFrame(requestAnimationFrameID); // Instruct the browser to stop calling requestAnimationFrame()'s callback.
return;
}
mySquare.transform.baseVal.getItem(0).setRotate(mySquare.currentTheta, 0, 0); // Access the transform object (that was appended to mySquare in the init() function) and use its setRotate method to rotate the square about the point (0, 0) (which is at the center of the SVG viewport).
mySquare.currentTheta += thetaDelta; // Place this line here so that the square isn't over rotated on the last call to doAnim().
requestAnimationFrameID = requestAnimationFrame(doAnim); // Call the doAnim() function about every 60 times per second (i.e., 60 FPS).
}
</script>
</body>
</html>
Perhaps the most difficult part of example 3 are the following two lines:
transformObject = svgElement.createSVGTransform(); mySquare.transform.baseVal.appendItem(transformObject);
The first line creates a generic transform object. The second line attaches this transform object to the mySquare node. This allows the mySquare object to inherit all the methods and properties associated with the transform object – in particular, the setRotate method. After this is done, we can rotate the mySquare square by simply calling its (newly acquired) setRotate method as follows:
mySquare.transform.baseVal.getItem(0).setRotate(mySquare.currentTheta, 0, 0);
As an aside, you can avoid the creation and appending of the transform object by adding a “no-op” transform attribute to the rect element; such as transform="matrix(1 0 0 1 0 0)":
<rect id="mySquare" x="-100" y="-100" width="200" height="200" rx="5" ry="5" transform="matrix(1 0 0 1 0 0)" style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;" />
This creates a transform object on the rectangle element, which you can then manipulate without having to first create and append one “on the fly”. The complete example follows:
Example 4 – No-op Transform Object
Live link:Example 4
<!DOCTYPE html>
<html>
<head>
<title>JavaScript SVG Animation</title>
<meta http-equiv="X-UA-Compatible" content="IE=Edge" /> <!-- Remove this line in production. -->
</head>
<body>
<svg width="800px" height="800px" viewBox="0 0 800 800">
<g transform="translate(400, 400)"> <!-- Create a Cartesian coordinate system (with the y-axis flipped) for the animated square. That is, place the origin at the center of the 800 x 800 SVG viewport: -->
<!-- A 200 x 200 square with the upper left-hand corner at (-100, -100). This places the center of the square
at the origin (0, 0). Note that the no-op transform attribute is necessary to generate a transform object
such that the setRotate() method can be utilized in the doAnim() function: -->
<rect id="mySquare" x="-100" y="-100" width="200" height="200" rx="5" ry="5"
transform="matrix(1 0 0 1 0 0)"
style=" fill: orange; stroke: black; stroke-width: 3; stroke-dasharray: 10, 5;" />
<!-- Represents the x-axis: -->
<line x1="-400" y1="0" x2="400" y2="0" style="stroke: black;" />
<!-- Represents the y-axis (although up is negative and down is positive): -->
<line x1="0" y1="-400" x2="0" y2="400" style="stroke: black;" />
</g>
</svg>
<script>
"use strict";
/* CONSTANTS */
var initialTheta = 0; // The initial rotation angle, in degrees.
var thetaDelta = 0.3; // The amount to rotate the square about every 16.7 milliseconds, in degrees.
var angularLimit = 90; // The maximum number of degrees to rotate the square.
/* GLOBALS */
var mySquare = document.getElementById("mySquare");
var requestAnimationFrameID;
mySquare.currentTheta = initialTheta; // The initial rotation angle to use when the animation starts.
requestAnimationFrameID = requestAnimationFrame(doAnim); // Start the animation loop.
function doAnim() {
if (mySquare.currentTheta > angularLimit) {
clearInterval(requestAnimationFrameID);
return;
}
mySquare.transform.baseVal.getItem(0).setRotate(mySquare.currentTheta, 0, 0); // Rotate the square about the point (0, 0), which is now at the center of the SVG viewport. Assumes a no-op transform attribute has been applied to the mySquare element, such as transform="matrix(1 0 0 1 0 0)".
mySquare.currentTheta += thetaDelta; // Increase the angle that the square will be rotated to, by a small amount.
requestAnimationFrameID = requestAnimationFrame(doAnim); // Call the doAnim() function about 60 time per second, or about once every 16.7 milliseconds until cancelRequestAnimation() is called.
}
</script>
</body>
</html>
In Example 4, we use an identity matrix as our “no-op” transform attribute to generate a transform object. We could have just as easily used transform=”rotate(0)” instead.
One advantage of Example 3 over Example 4 is that you don’t have to remember to add a “no-op” attribute to the rectangle element.
Now that we understand both scripting styles (DOM L2 and SVG DOM), we move on to more interesting animations – the following example attempts to model rotating friction gears. Imagine the rubber of two bicycle wheels rotating against one another. The rubber’s high coefficient of friction ensures that when one wheel rotates, so will the other. Here is an idealized version of this circular friction gear system:
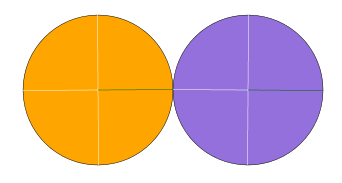
The code to generate this image is shown in the next example:
Example 5 – Two Gears
Live link:Example 5
<!DOCTYPE html>
<html>
<head>
<title>Two Animated Gears</title>
<meta http-equiv="X-UA-Compatible" content="IE=Edge"/> <!-- Remove this line in production. -->
</head>
<body>
<div align="center"> <!-- An inexpensive way to center everything. -->
<div style=" margin-bottom: 8px;">
<button id="startButton" type="button" onclick="startAnim();">
Start Animation
</button>
</div>
<svg id="svgElement" width="800px" height="800px" viewBox="0 0 800 800"> <!-- Give the svg element a name so that we can easily access it via JavaScript. -->
<rect x="0" y="0" width="100%" height="100%" rx="16" ry="16"
style="fill: none; stroke: black; stroke-dasharray: 10, 5;" />
<defs> <!-- Do not render the gear template, just define it. -->
<g id="gearTemplate"> <!-- Give this group of graphic elements a name so that it can be "called" from the <use> element. -->
<circle cx="0" cy="0" r="150" style="stroke: black;" />
<line x1="0" y1="-150" x2="0" y2="150" style="stroke: white;"/> <!-- From top to bottom, draw the vertical wheel "spoke". -->
<line x1="-150" y1="0" x2="0" y2="0" style="stroke: white;"/> <!-- Draw left half of the horizontal "spoke". -->
<line x1="0" y1="0" x2="150" y2="0" style="stroke: darkGreen;"/> <!-- Draw right half of the horizontal "spoke". -->
</g>
</defs>
<g transform="translate(400, 400)"> <!-- Create a Cartesian coordinate system (with the y-axis flipped) for the animated gears. That is, place the origin at the center of the 800 x 800 SVG viewport: -->
<use id="gear0" x="-150" y="0" xlink:href="#gearTemplate" style="fill: orange;" /> <!-- Use the previously defined gear template and position it appropriately. -->
<use id="gear1" x="150" y="0" xlink:href="#gearTemplate" style="fill: mediumPurple;" /> <!-- Same as the previous line but give this circle a different color. -->
</g>
</svg>
</div>
<script>
"use strict";
/* CONSTANTS */
var initialTheta = 0; // The initial rotation angle, in degrees.
var currentTheta = initialTheta; // The initial rotation angle to use when the animation starts.
var thetaDelta = 0.5; // The amount to rotate the gears every ~16.7 milliseconds or so, in degrees.
var angularLimit = 360; // The maximum number of degrees to rotate the gears.
/* GLOBALS */
var requestAnimationFrameID;
var transformObject = svgElement.createSVGTransform(); // Create a generic SVG transform object so as to gain access to its methods and properties, such as setRotate().
var gear0 = document.getElementById('gear0');
var gear1 = document.getElementById('gear1');
gear0.transform.baseVal.appendItem(transformObject); // Append the transform object to gear0, now the gear0 object has inherited all the transform object's goodness.
gear1.transform.baseVal.appendItem(transformObject); // Append the same generic transform object to gear1 - we just want gear1 to inherit all of it's goodness.
function startAnim() {
if (!startButton.startButtonClicked) // Don't allow multiple instance of the function specified by requestAnimationFrame to be invoked by the browser. Note that button.startButtonClicked will be undefined on first use, which is effectively the same as false.
{
/* Only do the following once per full animation: */
startButton.startButtonClicked = true; // A custom property is attached to the button object to track whether the button has been clicked or not.
requestAnimationFrameID = requestAnimationFrame(doAnim); // Start the animation loop.
}
}
function doAnim() {
if (currentTheta > angularLimit) {
startButton.startButtonClicked = false; // Let the user run the animation again if they choose.
currentTheta = initialTheta; // If we let the user run the animation multiple times, be sure to set currentTheta back to an appropriate value.
cancelAnimationFrame(requestAnimationFrameID); // Instruct the browser to stop calling requestAnimationFrame()'s callback.
return; // We have completed our animation, time to quit.
}
gear0.transform.baseVal.getItem(0).setRotate(currentTheta, -150, 0); // Rotate the 0th gear about the point (-150, 0).
gear1.transform.baseVal.getItem(0).setRotate(-currentTheta, 150, 0); // Rotate the 1st gear, note the minus sign on currentTheta, this rotates the gear in the opposite direction.
// gear0.setAttribute("transform", "rotate(" + currentTheta + ", -150, 0)"); // More cross-browser friendly, slightly less performant. Note that you don't technically need to append a transform object to each gear object, in init(), when using this line.
// gear1.setAttribute("transform", "rotate(" + -currentTheta + ", 150, 0)"); // More cross-browser friendly, slightly less performant. Note that you don't technically need to append a transform object to each gear object, in init(), when using this line.
currentTheta += thetaDelta; // Place this line here so that the gears are not over rotated on the last call to doAnim().
requestAnimationFrameID = requestAnimationFrame(doAnim); // Call the doAnim() function about every 16.7 milliseconds (i.e., about 60 frames per second).
}
</script>
</body>
</html>
In Example 5, we animated two graphic objects and added a Start Animation button, which caused quite a bit of code refactoring with respect to the rotating square in Example 4. In particular:
- Instead of creating SVG markup for two separate “gears”, we created a gear template that we can reuse as many times as we want to by using the
useelement. - To simplify things, we made
currentThetaa global variable so that its value can be applied to both gears. - A new function,
startAnim, was introduced. Clicking the Start Animation button invokes this function which starts the animation loop throughrequestAnimationFrame. - If the user clicked the Start Animation button multiple times, this would (without protection), invoke multiple instances of
doAnim, which makes the animation appear to run much faster than it should. To stop this undesirable behavior, we append the custom propertystartButtonClickedto the button object and set it totruewhen the button is first clicked. - In order to allow the user to restart the animation (after it completes), the following two lines were added to
doAnim:startButton.startButtonClicked = false; currentTheta = initialTheta;
These lines are executed only when the animation completes (that is, when
currentThetais greater thanangularLimit).
One of the issues with Examples 5 is that for each gear, you must individually call its setRotate method as well as remember where each gear’s center should be. This could become tedious if you had many such gears. One solution to this problem is to use an array of gears, as shown in Example 6 (Because of its length, the example code is not shown in this document. Use Internet Explorer\’s View source feature to view the live example instead). A screenshot of the example follows:
Example 6 – Seventeen Gears
Live link:Example 6
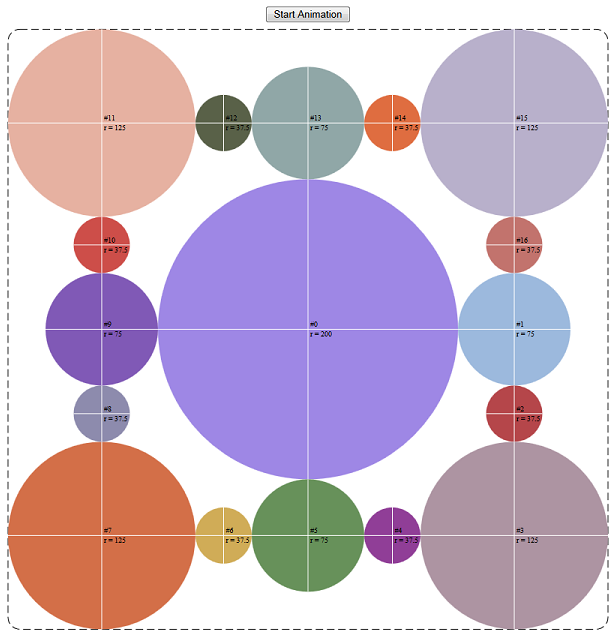
In the code for Example 6 animates 17 gears. As opposed to typing out 17 use elements, all with unique color and (x, y) value information (as was done in Example 5 for two gears), we programmatically build an array of gears containing this information as well as some other useful information:
- The radius of each gear (so that, among other things, we can calculate an appropriate rotational speed for the gear).
- The current angular position (in degrees) of each gear (that is,
currentAngle). - The name of each gear, and so on.
Additionally, we use the gear array to programmatically append appropriate elements to the DOM such that the gears are rendered on screen. That is, the JavaScript code appends the gear elements to the following “coordinateFrame” g element:
<g id="coordinateFrame" transform="translate(400, 400)"> <!-- Gear <g> elements will be appended here via JavaScript. --> </g>
The largest gear (“#0” above) is the drive gear. The drive gear rotates all the remaining gears, which are thus idler gears. Because there’s a single drive gear, we set its rotational speed (constants.driveGearSpeed = 0.3) and calculate the required speeds of the other gears based on it, as follows:
gears[i].currentAngle += (gears[i].clockwise * constants.driveGearSpeed * (gears[constants.driveGearIndex].r/gears[i].r));
First, each gear tracks its own angular position via its gears[i].currentAngle property. The direction a gear should rotate is determined by gears[i].clockwise (which is either 1 or -1). A given gear’s current angular position is simply the drive gear’s angular speed multiplied by the drive gear’s radius, divided by the current gear’s radius. Be aware that in the case of the drive gear itself, gears[constants.driveGearIndex].r/gears[i].r is 1, as it should be.
The other item to point out is the use of the custom button property startButtonClicked – this allows the button object to track its own current state – clicked or not.
If you have additional questions about Example 6, review the comments within the sample itself – every important line is fully described.
The next example extends Example 6 by replacing the single Start Animation button with additional user interface (UI) elements.
Example 7 – Seventeen Gears with Extended UI
Live link:Example 7
This example extends Example 6 by adding the following UI buttons:
.png)
Unsurprisingly, the Start, Pause, and Reset buttons start, pause and reset the animation; whereas the “ ” and “-” buttons increase and decrease the speed of the animation. This new UI necessitates a number of code changes, including:
- There is no longer a need for an angular limit – we let the animation run until the user clicks the Pause or Reset button. To avoid potential variable overflow, the following code was used:
if (gears[i].currentAngle >= 360) gears[i].currentAngle -= 360;
This keeps each gear’s
currentAnglevalue small without affecting the meaning ofcurrentAngle. That is, a circle rotated 362 degrees looks the same as a circle rotated 2 degrees (for example, 362 – 360 = 2 degrees).
Example 8 – Seventeen Gears with Audio
Live link:Example 8
Using the HTML5 audio element, this example extends the previous example by adding a sound effect that linearly increases or decreases in tempo as the “ ” and “-“ buttons are clicked. And given the possibly annoying nature of any sound effect, we’ve also added a convenient Sound Off button:
.png)
The Example 8 audio code is relatively straightforward and well commented. The only function possibly needing additional explanation is calculatePlaybackRate, which returns an appropriate audio file playback rate given the current rotational speed of the drive gear. To help explain how this is done, consider the following graph:
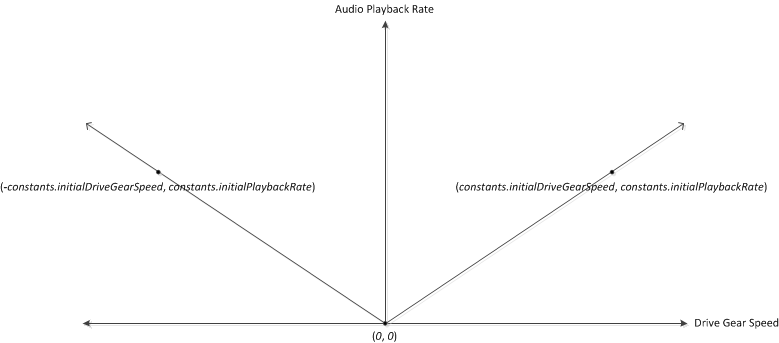
The x-axis represents the current rotational speed of the drive gear (which can be positive or negative). The y-axis represents an appropriate audio file playback rate (which can only be positive). We know that when the drive gear speed is zero, the audio playback rate should also be zero (that is, no sound). And from our initializing constants, we know that when the drive gear speed is constants.initialDriveGearSpeed, the audio playback rate is constants.initialPlaybackRate. We now have two points: (0, 0) and (constants.initialDriveGearSpeed, constants.initialPlaybackRate). Because two points define a line (and because we want a linear response), we can easily derive the equation used in calculatePlaybackRate by calculating the slope of the line (m) and multiplying it with the absolute value of the current drive gear speed to obtain the correct audio file playback rate (See the comments in calculatePlaybackRate for more information).
The next logical step might be to add additional gears to Example 8. Because the example’s code uses an array of gear objects, one need only tack on appropriately sized and positioned gears to the array to increase the total number of gears in the animation. This is left as an exercise to the reader and should significantly help your understanding of the techniques presented in this topic.

